Déchiffrage du message dans le logo du podcast La French Connection
13 December 2023
- Minkowski / Institute for Security Through Obscurity Québec, Canada
Résumé
Depuis ses débuts, le logo du podcast La French Connection arbore un message chiffré. Bien des gens ont rêvé de percer le mystère de ce chiffre. Avis à ceux qui ne veulent pas briser la magie, ne lisez point une ligne de plus car ce texte dévoile les secrets et le message derrière ce logo. (1)
Analyse
Les amateurs du podcast La French Connection ont remarqué depuis longtemps que le logo du dit podcast présente, en son bas, une mystérieuse inscription qui recèle sans aucun doute un message secret (Figure 1).
Le message chiffré
Le mystérieux chiffre est composé de 25 nombres hexadécimaux. Il est souvent plus facile de convertir les nombres hexadécimaux en nombre décimaux. CyberChef se charge très bien de ce genre de besogne (Table 1).

Figure 1 : Logo du podcast La French Connection.
Table 1 : Mystérieux chiffre.
4E 39 44 60 35 63 3B 19 24 55 62 3A 2E 4F 56 42 4F 2D 21 3F 62 1C 26 3C 5F
78 57 68 96 53 99 59 25 36 85 98 58 46 79 86 66 79 45 33 63 98 28 38 60 95
Fréquences
Puisque nous mettons déjà à profit CyberChef, aussi bien en profiter pour faire une analyse en fréquence. La Figure 2 montre le résultat de cette analyse. On constate que sur 25 nombres, seulement deux sont répétés (4F et 62). En même temps, la séquence n’est pas aléatoire puisque les valeurs ne sont pas réparties uniformément sur la plage des 256 nombres possibles (de 00 à FF).
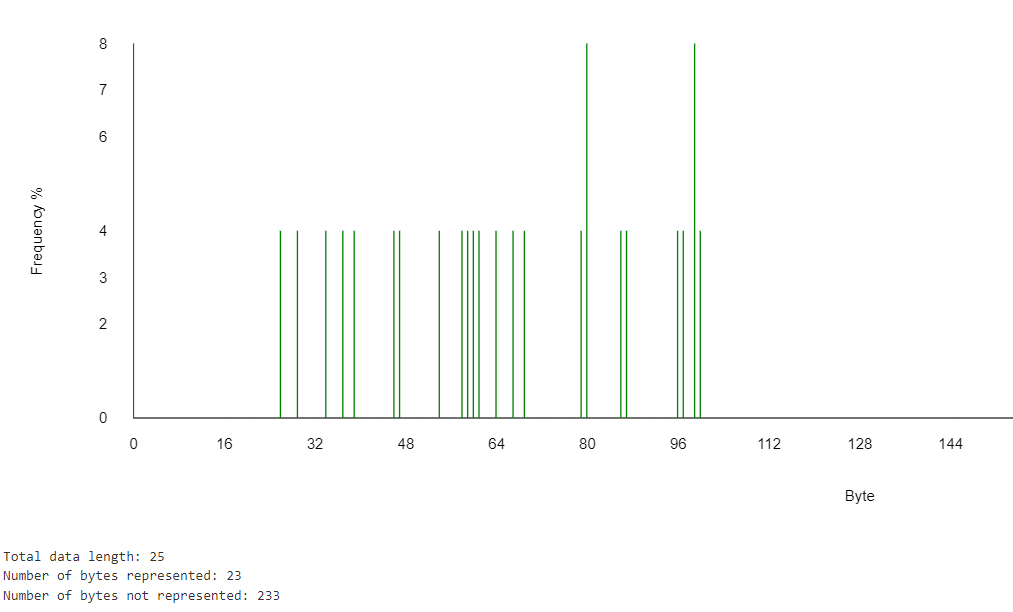
Figure 2 : Analyse de la fréquence des nombres.
Ces résultats nous permettent d’exclure un chiffrement moderne ou une fonction de hachage qui produirait des données plus uniformes. De plus, on n’a pas non plus affaire à un simple chiffre de substitution puisqu’il y a peu de répétitions. Le message chiffré étant très court, il est difficile de faire une analyse statistique plus poussée ou d’utiliser la force brute sans avoir identifié la méthode de chiffrement.
En regardant plus attentivement les nombres décimaux, on remarque qu’aucun ne se termine par 1, 2 ou 4. De plus, les chiffres des unités ne sont pas répartis uniformément, tel qu’illustré à la Table 2. La répartition du chiffre des dizaines est un peu plus uniforme, mais on note l’absence de tout chiffre plus petit que 20 (Table 3).
Table 2 : Répartition du chiffre des unités.
Unité %
0 4
3 12
5 16
6 20
7 4
8 28
9 16
Table 3 : Répartition du chiffre des dizaines.
Dizaine %
2 8
3 12
4 8
5 16
6 16
7 12
8 8
9 20
À la recherche du chiffre perdu
Avec les quelques informations obtenues, il est possible d’explorer plusieurs pistes pour tenter d’identifier le chiffrement utilisé. Les nombres du chiffre ont très certainement été créés à l’aide de règles mathématiques simples qui leurs confèrent les caractéristiques observées. Un bon endroit pour débuter la recherche pour identifier le chiffre est dCode. Ce site une ressource précieuse pour en apprendre plus sur les codes et le chiffrement. Il offre non seulement des descriptions très détaillées de plusieurs dizaines de chiffremements classiques, mais aussi des outils pour encoder, décoder et briser certains d’entre eux.
Polybe
Nous avons probablement affaire à un chiffre de substitution ou de transposition qui inclu des éléments additionnels pour rendre le déchiffrage plus difficile. La méthode la plus amusante pour identifier le chiffrement utilisé est de passer de longues heures à explorer les différents chiffres classiques, à lire leurs descriptions et à chiffrer et déchiffrer différents messages. C’est aussi la méthode demandant le plus de temps. Si vous l’utilisez, vous finirez probablement par tomber sur le chiffre de Polybe qui utilise le carré de Polybe, une grille de 5x5 associant chacune des lettres de l’alphabet à un nombre entre 11 et
- La Table 4 montre un carré possible. Comme il y a 26 lettres à l’alphabet, il faut en sacrifier une. Dans ce cas-ci on sacrifie le Z mais le J, V ou W sont aussi fréquemment rejetés.
Table 4 : Carré de Polybe.
1 2 3 4 5
1 A B C D E
2 F G H I J
3 K L M N O
4 P Q R S T
5 U V W X Y
Pour chiffrer un message à l’aide d’un carré de Polybe, il suffit de trouver la lettre dans le tableau et de la remplacer par le nombre formé par le numéro de ligne suivit par le numéro de colonne. Par exemple, la lettre Q sera remplacée par le nombre 42.
Polybe sur les stéroïdes
Afin de rendre la tâche plus difficile aux curieux, il est possible d’utiliser une clé pour changer l’ordre des lettres de la grille. Le mot utilisé doit avoir des lettres distinctes. On écrit les lettres de ce mot secret au haut de la grille et on continue avec les lettres restantes. Par exemple, avec la clé HACK on aurait le carré présenté en Table 5.
Table 5: Carré de Polybe avec la clé HACK.
1 2 3 4 5
1 H A C K B
2 D E F G I
3 J L M N O
4 P Q R S T
5 U V W X Y
Le chiffre de Polybe présente une régularité dans les nombres utilisés, ce qui le rend facilement identifiable puisque seuls les nombre 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55 sont utilisables.
Polybe ou pas Polybe? Là est la question!
Bien que le chiffre de Polybe présente des similitudes avec les caractéristiques de notre message, les nombres possibles ne correspondent pas. Nous avons donc affaire à un autre chiffre ou à une variation du chiffre de Polybe avec une grille différente.
En s’éduquant un peu plus sur le chiffre de Polybe, on constate qu’il est souvent associé au chiffre des Nihilistes qui est un surchiffrement du carré de Polybe. On peut reconnaitre le chiffre des Nihilistes grâce aux indices suivants:
-
Contient uniquement des nombres entre 22 et 110.
-
Ne contient aucun des nombres suivants:
21, 31, 41, 51, 61, 71, 81, 91, 101. -
Le chiffre est associé à une quelconque référence à la Russie.
Mini OSINT
Les deux premières caractéristiques correspondent parfaitement au message secret au bas du logo, mais une mention quelconque de la Russie dans un épisode confirmerait le tout. Un peu de Google Fu ceinture blanche (logo site:securite.fm) nous révèle qu’on mentionne le message encodé dans le logo à l’épisode 0x017 (aux environs de la minute 40), tel qu’illustré à la Figure 3. Lors de cet épisode Damien, toujours gourmand, nous donne un indice: "Poutine"... À moins qu’il fasse référence à un autre type de "Putin", beaucoup moins digeste.

Figure 3 : L’épisode 0x017 mentionne le mystère du logo.
Chiffre des Nihilistes
Rendu célèbre par son utilisation par les nihilistes russes du 19ième siècle. Ce chiffre est simple à mémoriser et permet de transmettre un message de plusieurs façons. Par exemple, les prisonniers russes transmettaient des messages de ce type en cognant sur les murs de leurs cellules un nombre de fois qui correspondait à la rangée puis à la colonne de chaque lettre.
Fonctionnement
Le fonctionnement du chiffre des Nihilistes est simple:
-
On choisit un carré de Polybe, avec les lettres potentiellement dans le désordre grâce à une clé convenue d’avance. Par exemple, le carré de la Table 5.
-
On encode le message avec la grille. Chaque lettre se voit attribuée un chiffre correspondant à une ligne et une colonne. Le message "MESSAGESECRET" deviendrait par exemple: 33 22 44 44 12 24 22 44 22 13 43 22 45.
-
On choisit une clé de surchiffrement et on l’encode avec le carré de Polybe. Si on choisit "PLANET" comme clé, on aura 41 32 12 34 22 45.
-
On réécrit la clé encodée autant de fois que nécessaire sous le message encodé et on additionne les deux nombres comme dans la Table 6.
Table 6 : Surchiffrement.
M E S S A G E S E C R E T
---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
33 22 44 44 12 24 22 44 22 13 43 22 45
41 32 12 34 22 45 41 32 12 34 22 45 41
74 54 56 78 34 69 63 76 34 47 65 67 86
On obtient alors un chiffrement par substitution auquel on additionne une clé de façon répétée. Au final, on aura un chiffrement polyalphabétique fractionné puisque deux lettres identiques peuvent être encodées de façon différente selon leur position dans le message.
Vulnérabilités
Le chiffre des Nihilistes comporte de multiples vulnérabilités dont celles ci-dessous:
-
La clé de surchiffrement est répétée. Quand le message chiffré est plus long que cette clé, on peut observer des similitudes entre les blocs de texte de même longueur que la clé.
-
Il y a un nombre limité de combinaisons pour les additions. Par exemple, le chiffre 80 ne peut être obtenu qu’avec les additions $25+55$ ou $35+45$.
-
Plus les nombres sont grands ou petits, plus les possibilités sont limitées. Par exemple, 22 ou 110 ne peuvent être obtenus que si la lettre encodée est la même que celle de la clé de surchiffrement et que cette lettre est soit dans le coin supérieur gauche ou le coin inférieur droit de la grille, respectivement.
-
Un nombre ayant un 0 à la position des unités indique que les nombres additionnés proviennent de la dernière colonne.
-
Similairement, un nombre ayant un 2 à la position des unités provient d’une addition de nombres de la première colonne.
-
Une fois la longueur de la clé identifiée et un espace de clé réduit, on peut trouver la clé (si c’est un mot), par déduction ou avec un dictionnaire.
-
Une fois la clé de surchiffrement trouvée, le problème se réduit à un simple chiffre de substitution, un chiffre de Polybe.
La cryptanalyse du chiffre des Nihilistes sera grandement facilitée si le message codé est long et/ou si on possède un autre message décodé qui aurait été chiffré avec la même grille et la même clé de surchiffrement. Malheureusement, dans le cas présent, on n’a aucun de ces deux éléments facilitateurs.
Déchiffrement
Il y a très peu de répétitions dans le message codé, 78 57 68 96 53 99 59 25 36 85 98 58 46 79 86 66 79 45 33 63 98 28 38 60 95, ce qui indique que la clé de surchiffrement n’est probablement par trivialement courte (1, 2 ou 3 caractères).
Longueur de la clé
La première étape est de déterminer la longueur de la clé de surchiffrement ce qui nous donnera la période du chiffre. Un chiffre aura une période de 4 si une clé de 4 caractères est répétée pour le chiffrement puisque chaque bloc de 4 lettres utilisera la même clé.
Pour déterminer la longueur de la clé, on va créer des tableaux avec un nombre de colonnes correspondant à la longueur de clé que l’on désir tester. Par exemple, si on veut vérifier si une clé de 6 caractères est possible, on doit créer la Table 7 de 6 colonnes et y placer le message chiffré dans l’ordre.
Table 7 : Tableau pour tester si une clé de 6 caractères est possible.
78 57 68 96 53 99
59 25 36 85 98 58
46 79 86 66 79 45
33 63 98 28 38 60
95
On doit créer un tableau de ce genre pour toutes les longueurs de clés de surchiffrement qu’on veut tester. Dans notre cas, entre 1 et 25 colonnes.
Pour chaque colonne d’un tableau, on applique l’algorithme ci-dessous. D’abord au chiffre des dizaines, puis au chiffre des unités. Si pour une colonne, cet algorithme retourne faux soit pour le chiffre des dizaines ou des unités, c’est qu’aucune addition n’est possible pour les combinaisons de nombres dans la colonne. La clé de surchiffrement ne peut donc avoir la longueur supposée.
Essentiellement, on vérifie que la différence entre le chiffre maximum et minimum est plus petite que 5. Si ce n’est pas le cas, c’est impossible qu’un même chiffre (entre 1 et 5) ait pu surencoder le chiffre des unités ou dizaines. Par exemple, si les chiffres des unités pour une colonne sont 2, 4, 7, 3, 4, la différence entre 7 et 2 est de
- Or il est impossible de trouver deux chiffres tels que $x_1 + y = 7$ et $x_2 + y = 2$ où $1\leq x_i \leq 5$ et $1\leq y \leq 5$
array $A \gets$ chiffres des unités ou dizaines
for all 𝑛 ∈ {0, . . . , 𝑎𝑟𝑟𝑎𝑦𝑙𝑒𝑛𝑔𝑡ℎ − 1} do
if 𝐴[𝑖] == 0 then
$A[i] \gets 10$
end if
end for
return max(A) - min(A) \< 5
Si on revient à la Table 7, on constate que les chiffres des dizaines pour la première colonne sont 7, 5, 4, 3, 9. On a une différence de 6 entre les chiffres maximum et minimum, donc aucune clé de 6 caractères n’aurait pu être utilisée.
Si on applique cette règle pour des tableaux de 2 à 25 rangées (à l’aide d’un script Python maison), on obtient des longueurs de clés possibles de 10, 20, 22, 23, 24 ou 25. Comme le message a 25 caractères, les clés de longueur entre 20 et 25 sont considérées comme possibles puisque dans ces cas la majorité des colonnes ne contiendront qu’un nombre. Par contre, elles sont peu probables puisque si la longueur de la clé est près de la longueur du message, on aura presque un chiffre de Vernam (one-time pad) ce qui serait pratiquement impossible à décoder sans connaitre la clé.
Dans ces circonstances, la longueur de la clé est fort probablement de 10.
Espace de clé
Une fois la longueur de la clé établie, on peut tenter de réduire l’espace de clé. En effet, avec le chiffre des Nihilistes, ce ne sont pas toutes les clés de 10 caractères qui sont possibles, mais seulement un nombre réduit de celles-ci. Pour limiter le nombre de clés possibles on a besoin de la Table 8 avec autant de colonnes que la longueur de la clé.
Table 8 : Tableau de 10 colonnes.
78 57 68 96 53 99 59 25 36 85
98 58 46 79 86 66 79 45 33 63
98 28 38 60 95
Pour chacune des colonnes de ce tableau, on doit appliquer l’algorithme suivant qui produira la liste des nombres possiblement utilisés pour surchiffrer une colonne. Encore une fois, c’est une conséquence directe de l’utilisation du carré de Polybe qui limite le nombre des unité ou dizaines à un chiffre entre 1 et 5.
array $col \gets$ une colonne du tableau
$dizaineMin \gets 1$
$dizaineMax \gets 5$
$uniteMin \gets 1$
$uniteMax \gets 5$
for all 𝑛 ∈ 𝑐𝑜𝑙 do
$unite \gets n \mod 10$
if $unite == 0$ then
$uniteMin \gets 5$
$uniteMax \gets 5$
else if $unite < 7$ then
$uniteMin \gets 1$
$uniteMax \gets unite - 1$
else
$uniteMin \gets unite - 5$
$uniteMax \gets 5$
end if
array $unitesPossibles \gets \{uniteMin, \dots, uniteMax\}$
$dizaine \gets floor(n/10) \mod 10$
if $dizaine == 0$ then
$dizaineMin \gets 5$
$dizaineMax \gets 5$
else if $dizaine < 7$ then
$dizaineMin \gets 1$
$dizaineMax \gets dizaine - 1$
else
$dizaineMin \gets dizaine - 5$
$dizaineMax \gets 5$
end if
array $dizainesPossibles \gets \{dizaineMin, \dots, dizaineMax\}$
end for
return $combinaisons(dizainesPossibles, unitesPossibles)$
Si on applique cet algorithme à chaque colonne de la Table 8 , on obtient les possibilités de la Table 9 pour chacun des caractères de la clé de surchiffrement.
Table 9 : Espace de clé.
Position Possibilités
1 43, 44, 45, 53, 54, 55
2 13, 14, 15
3 13, 14, 15, 23, 24, 25
4 45
5 41, 42
6 44, 45, 54, 55
7 24, 25, 34, 35, 44, 45
8 11, 12, 13, 14
9 11, 12, 21, 22
10 31, 32, 41, 42, 51, 52
Même si tous ces calculs sont faisables à la main, un script Python peut être une aide importante tant au point de vue temps, que santé mentale.
Des chiffres
Pour ce chiffre, on a donc une clé de 10 caractères chaque caractère ayant respectivement 6, 3, 6, 1, 2, 4, 6, 4, 4, et 6 possibilités. Le nombre de combinaisons possibles est de $6 \times 3 \times 6 \times 1 \times 2 \times 4 \times 6 \times 4 \times 4 \times 6 = 497664$. Parmi ces combinaisons, beaucoup ne sont pas des mots. On pourrait commencer par les exclure mais, au final, si la clé est aléatoire nous avons 497664 clés à tester.
De plus, si on ne veut pas devoir valider manuellement chaque test de déchiffrage, il faudrait automatiser le tout en comparant chaque bloc de 4 caractères d’une tentative de décodage aux quadrigrammes français et anglais (on présume que le message est dans une de ces deux langues) qui sont au nombre d’environ 400000 chacun. Notons qu’il y a 22 blocs de 4 caractères possibles dans une séquence de 25 caractères.
Finalement, rien ne nous certifie qu’un carré de Polybe totalement aléatoire n’a pas été utilisé pour la substitution initiale. Pour 26 lettres on a $26! \approx 4 \times 10^{26}$ carrés possibles.
On aura approximativement $497644 \times 400000 \times 400000 \times 22 \times 4 \times 10^{26} \approx 7 \times 10^{44}$ tests à faire.
Ça fait beaucoup de chemins à explorer, il faut donc réduire encore plus cet espace d’exploration en faisant plusieurs suppositions.
Suppositions
Pour débuter, on fera les suppositions suivantes:
-
La clé de surchiffrement est un mot. Probablement relié au podcast.
-
Le carré de Polybe utilisé est un des quelques carrés les plus connus (avec les lettres de l’alphabet pratiquement dans l’ordre).
-
La langue utilisée pour la clé et le message original est soit le français ou l’anglais.
-
L’algorithme des Nihilistes utilisé pour chiffer le message n’a pas été modifié pour compliquer le déchiffrement.
Trouver la clé de surchiffrement
Fort de ces suppositions, on peut enfin s’attaquer à la clé de surchiffrement. On présume que le carré de Polybe le plus commun, où on omet la lettre "J", a été utilisé (Table 10). Encoder le message avec ce carré impliquerait l’utilisation des lettres de la Table 11 pour chiffrer la clé.
Table 10 : Carré de Polybe présumément utilisé.
1 2 3 4 5
1 A B C D E
2 F G H I K
3 L M N O P
4 Q R S T U
5 V W X Y Z
Table 11 : Lettres possibles pour la clé.
1 2 3 4 5 6 7 8 9 10
S C C U Q T I A A L
T D D R U K B B M
U E E Y O C F Q
X H Z P D G R
Y I T V
Z K U W
Les 10 lettres les plus communes dans les mots français sont e, a, i, s, n, r, t, o, l, u alors qu’en anglais il s’agit de e, t, a, o, i, n, s, h, r, d. Ne conservons pour l’instant que les lettres les plus communes pour les deux langues. En faisant ceci, on se rend presque immédiatement compte, si on a déjà joué au scrabble ou fait des mots cachés, qu’on a presque le mot SECURITÉ ou encore SECURITY (Table 12). Ce n’est très certainement pas un hasard.
Table 12 : Lettres possibles épurées.
1 2 3 4 5 6 7 8 9 10
S C U T I A A L
T D D R U
U E E O
H D R
I T
U
Une bonne façon de vérifier si on est sur la bonne voie est d’utiliser cette clé de surchiffrement partielle pour décoder le message. L’utilisation de dCode accélère grandement ce genre de test puisqu’il permet de modifier rapidement soit le carré de Polybe, soit la clé. Comme il nous manque quelques lettres à la clé pour former un mot, on va les remplacer arbitrairement par la première lettre de chaque colonne. On obtient la clé SECURTTAAL. En utilisant celle-ci et la Table 10 pour tenter de déchiffrer le message on obtient PRZVAZEDKYZSNOTGPOGMZCKEX.
On remarque un petit mot anglais et quelques bigrammes communs en
anglais dans le message partiellement décodé:
PRZVAZEDKYZSNOTGPOGMZCKEX.
C’est un grand pas puisqu’on a identifié la langue du message original. De plus, il y a plus de lettres "Z" qu’il ne faudrait dans ce message, ce qui laisse croire qu’il y a un problème avec le carré de Polybe utilisé. En consultant la liste des 10 lettres les plus communes en anglais on remarque que le "I", la cinquième lettre la plus utilisée dans cette langue, n’apparait jamais alors que le "Z" apparait à quatre reprises. Si on inverse les positions du "I" et du "Z" dans le carré de Polybe et qu’on tente à nouveau de décoder le message on obtient un message partiellement décodé avec encore plus de mots et mots partiels PRIVAIEDKYISNOTGPOGMICKEX.
À ce point, il est beaucoup plus facile d’essayer quelques autres clés que de tenter de modifier le carré de Polybe. En essayant avec les clés SECURITEAL et SECURITYAL on obtient:\
SECURITEAL: PRIVATE?KYISNOTAP?GMICKEX
SECURITYAL: PRIVATE?BIUYNNTQC?BHKVMVI?
La première tentative de clé, avec le mot en français, est clairement mieux même si deux lettres sont impossibles à décoder avec le carré de Polybe utilisé. Pour les deux dernières lettres de la clé, on peut soit utiliser la force brute et tester toutes les combinaisons possibles ou se souvenir (grâce à notre mini OSINT) que le site internet du podcast est securite.fm.
Avec la clé de surchiffrement "SECURITEFM", on décode le message PRIVATE?EXISNOTAP?BLICKEX qu’on peut deviner être "PRIVATEKEXISNOTAPUBLICKEY". Cependant, le message n’est pas totalement décodable avec cette clé. On peut facilement améliorer la situation en inversant les lettres "X" et "Y" dans le carré de Polybe pour obtenir la Table 13.
Table 13 : Carré de Polybe final.
1 2 3 4 5
1 A B C D E
2 F G H Z K
3 L M N O P
4 Q R S T U
5 V W Y X I
Avec cette clé et ce carré de Polybe, deux nombres dans notre séquence de chiffres initiale ne peuvent être décodés 78 57 68 96 53 99 59 25 36 85 98 58 46 79 86 66 79 45 33 63 98 28 38 60 95. Ils correspondent aux lettres aux positions 8 et 18 du message. Avec la clé de surchiffrement actuelle, le nombre 25 devrait être 10 puisqu’on devrait soustraire 15 (à cause du "E") et le nombre 45 devrait être 30, pour la même raison.
Or 10 et 30 ne peuvent être obtenus avec la clé et le carré de Polybe trouvés. Cependant, les nombres 25 et 45 correspondent aux lettres manquantes "K" et "U". Ces deux lettres n’ont tout simplement pas été surchiffrées avec la clé! Il s’agit soit d’une erreur involontaire ou d’une tentative de rendre le déchiffrement du message plus difficile. Au final, tous seront d’accord avec le message secret: "private key is not a public key".
Solution officielle
Après avoir validé le message secret avec les instances officielles de la French Connection. Les hautes autorités m’ont transmise la solution officielle que je vous communique. Un certain point dans celle-ci peut nous laisser perplexe :
- Texte à encoder: PRIVATEKEYISNOTAPUBLICKEY
- Jeu de caractères de clé: ABCDEFGHIJKLMNOPQRSTUVVVXYZ (w = VV)
- Clé: SECURITE.FM
- Encoder la réponse en hexa
Le tout a été encodé à l’aide d’un outil non spécifié, utilisant très certainement le chiffre des Nihilistes. Le point délicat dans cette solution étant bien évidement le point «.» entre SECURITE et FM. Il n’apparait nulle part dans les caractères utilisés dans le chiffre. Pourtant, l’outil utilisé a bien chiffré le message. Cette clé non conventionnelle explique probablement pourquoi deux lettres n’étaient pas encodées tel qu’attendu.
Ceci illustre la difficulté de déchiffrer un message encodé avec un algorithme et des outils inconnus. On n’est jamais à l’abris des surprises.
Références
-
https://alexbarter.com/cryptanalysis/breaking-nihilist-substitution-cipher/
-
http://www.benburlingham.com/core/articles/nihilist-cipher.html
(1) Ce travail est sujet à la licence WTFPL. Visitez http://www.wtfpl.net/ pour une copie complète de cette licence.